I suppose that the reason I have a been in my bonnet on this issue is that a I really hate audio bullshit and bollocks reviewers who have made a living out of false pretenses on their super hearing with crap like this idiot:
Best CD players 2022: CD players for every budget
lines like.....dynamic expressions, rhythmic ability, expressive punchy dynamics, powerful and articulate lows, clear elegant vocals, layered and articulate soundscape.....waffle waffle, lie.
We have a whole industry being reviewed by these frauds and an unquestioning public being sold on stuff with no additional gain. Recently on a facebook surround forum (I am not a facebook type really) someone asked me if the new SM 3 would sound any better that the old SM1.....I basically replied NUP. Having said that I really prefer the new ones with the metal box and KNOBS!!
Really spend your budget on where you will hear a difference......speakers, room and amplifiers (if you are running brutes like ribbons or electrostatics- soft clipping etc).
Here is an excellent article, please read!
What you think you know about bit-depth is probably wrong
What you think you know about bit-depth is probably wrong
In the modern age of audio, you can't move for mention of "Hi-Res" and 24 bit depth "Studio Quality" music, but does anyone understand what that actually means?
By
•
July 13, 2021
In the modern age of audio, you can’t move for mentions of “Hi-Res” and 24-bit “Studio Quality” music. If you haven’t spotted the trend in high-end smartphones—Sony’s
LDAC Bluetooth codec—and streaming services like
Qobuz, then you really need to start reading this site more.
The promise is simple—superior listening quality thanks to more data, aka bit depth. That’s 24 bits of digital ones and zeroes versus the puny 16-bit hangover from the CD era. Of course, you’ll have to pay extra for these higher quality products and services, but more bits are surely better right?
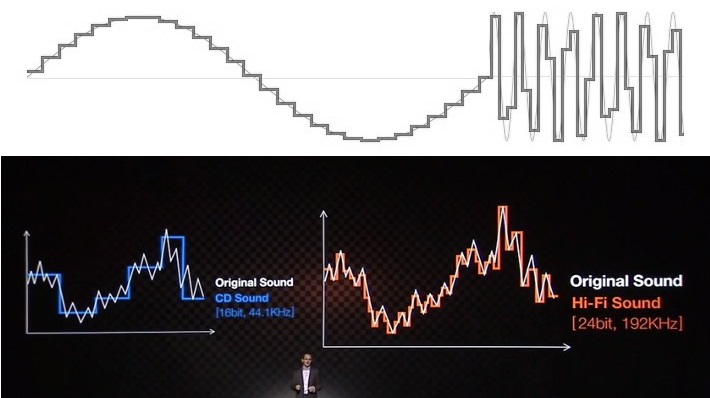
“Low res” audio is often shown off as a staircase waveform. This is not how audio sampling works and isn’t what audio looks like coming out of a device.
Not necessarily. The need for higher and higher bit depths isn’t based on scientific reality, but rather on a twisting of the truth and exploiting a lack of consumer awareness about the science of sound. Ultimately, companies marketing 24-bit audio have far more to gain in profit than you do in superior playback quality.
Editor’s note: this article was updated on July 13, 2021, to update some technical wording and to add a contents menu.
Bit depth and sound quality: Stair-stepping isn’t a thing
To suggest that 24-bit audio is a must-have, marketers (and many others who try to explain this topic) trot out the very familiar audio quality stairway to heaven. The 16-bit example always shows a bumpy, jagged reproduction of a sine-wave or other signal, while the 24-bit equivalent looks beautifully smooth and higher resolution. It’s a simple visual aid, but one that relies on the ignorance of the topic and the science to lead consumers to the wrong conclusions.
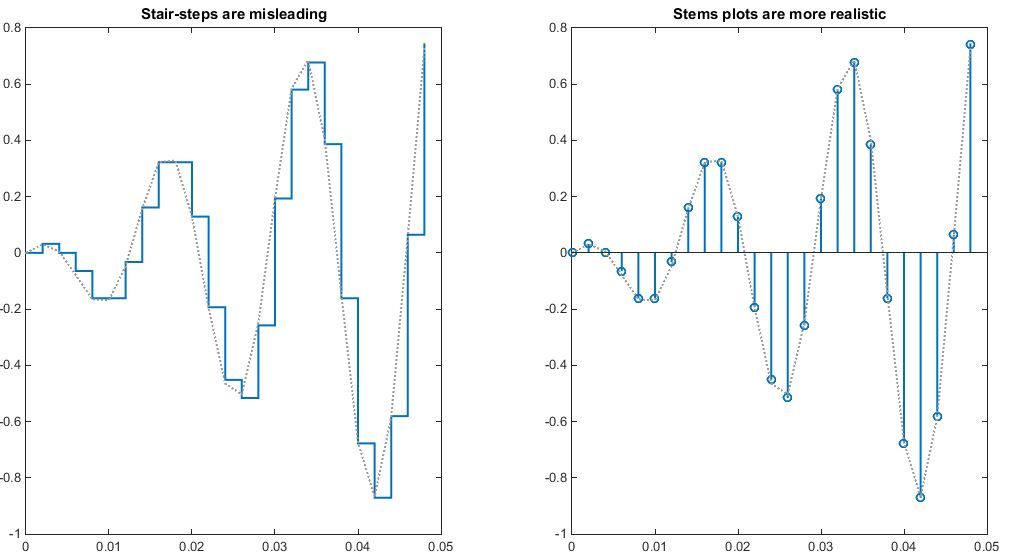
Before someone bites my head off, technically speaking these stair-step examples do somewhat accurately portray audio in the digital domain. However, a stem plot/lollipop chart is a more accurate graphic to visual audio sampling than these stair-steps. Think about it this way—a sample contains an amplitude at a very specific point in time, not an amplitude held for a specific length of time.
The use of stair graphs is deliberately misleading when stem charts provide a more accurate representation of digital audio. These two graphs plot the same data points but the stair plot appears much less accurate.
However, it’s correct that an analog to digital converter (ADC) has to fit an infinitely variable analog audio signal into a finite number of bits. A bit that falls between two levels has to be rounded to the closest approximation, which is known as quantization error or quantization
noise. (Remember this, as we’ll come back to it.)
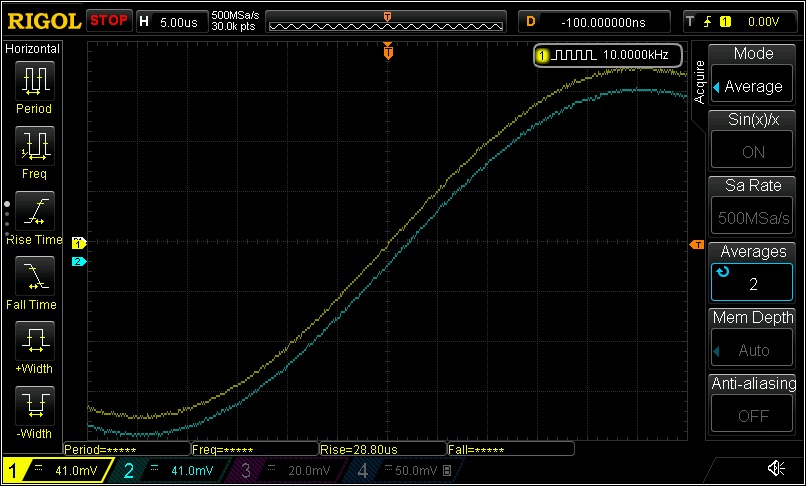
However, if you look at the audio output of any audio digital to analog converter (
DAC) built this century, you won’t see any stair-steps. Not even if you output an 8-bit signal. So what gives?
An 8-bit, 10kHz sine wave output captured from a low-cost Pixel 3a smartphone. We can see some noise but no noticeable stair-steps so often portrayed by audio companies.
First, what these stair-step diagrams describe, if we apply them to an audio output, is something called a
zero-order-hold DAC. This is a very simple and cheap DAC technology where a signal is switched between various levels every new sample to give an output. This is not used in any professional or half-decent consumer audio products. You might find it in a $5 microcontroller, but certainly not anywhere else. Misrepresenting audio outputs in this way implies a distorted, inaccurate waveform, but this isn’t what you’re getting.
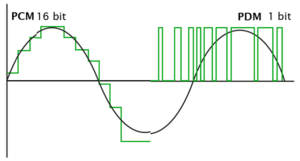
In reality, a modern ∆Σ DAC output is an oversampled 1-bit PDM signal (right), rather than a zero-hold signal (left). The latter produces a lower noise analog output when filtered.
Audio-grade ADCs and DACs are predominantly based on
delta-sigma (∆Σ) modulation. Components of this caliber include interpolation and oversampling, noise shaping, and filtering to smooth out and reduce noise. Delta-sigma DACs convert audio samples into a 1-bit stream (pulse-density modulation) with a very high sample rate. When filtered, this produces a smooth output signal with noise pushed well out of audible frequencies.
In a nutshell: modern DACs don’t output rough-looking jagged audio samples—they output a bit stream that is noise filtered into a very accurate, smooth output. This stair-stepping visualization is wrong because of something called “quantization noise.”
Understanding quantization noise
In any finite system, rounding errors happen. It’s true that a 24 bit ADC or DAC will have a smaller rounding error than a 16-bit equivalent, but what does that actually mean? More importantly, what do we actually hear? Is it distortion or fuzz, are details lost forever?
It’s actually a little bit of both depending on whether you’re in the digital or analog realms. But the key concept to understanding both is getting to grips with noise floor, and how this improves as bit-depth increases. To demonstrate, let’s step back from 16 and 24 bits and look at very small bit-depth examples.
The difference between 16 and 24 bit depths is not the accuracy in the shape of a waveform, but the available limit before digital noise interferes with our signal.
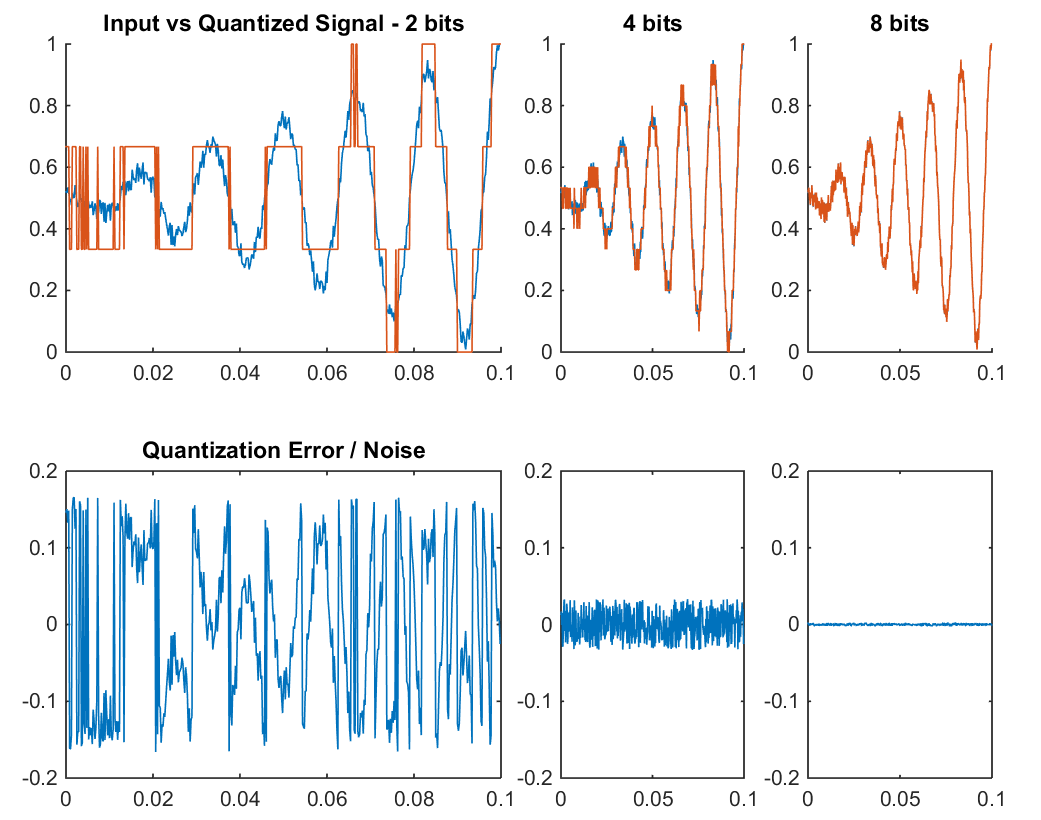
There are quite a few things to check out in the example below, so first a quick explanation of what we’re looking at. We have our input (blue) and quantized (orange) waveforms in the top charts, with bit depths of 2, 4, and 8 bits. We’ve also added a small amount of noise to our signal to better simulate the real world. At the bottom, we have a graph of the quantization error or rounding noise, which is calculated by subtracting the quantized signal from the input signal.
Quantization noise increases the smaller the bit depth is, through rounding errors.
Increasing the bit depth clearly makes the quantized signal a better match for the input signal. However that’s not what’s important, observe the much larger error/noise signal for the lower bit depths. The quantized signal hasn’t removed data from our input, it’s actually added in that error signal.
Additive Synthesis tells us that a signal can be reproduced by the sum of any other two signals, including out of phase signals that act as subtraction. That’s how noise cancellation works. So these rounding errors are introducing a new noise signal.
This isn’t just theoretical, you can actually hear more and more noise in lower bit-depth audio files. To understand why, examine what’s happening in the 2-bit example with very small signals, such as before 0.2 seconds. Click here for a
zoomed-in graphic. Very small changes in the input signal produce big changes in the quantized version. This is the rounding error in action, which has the effect of amplifying small-signal noise. So once again, noise becomes louder as bit-depth decreases.
Quantization doesn't remove data from our input, it actually adds in a noisy error signal.
Think about this in reverse too: it’s not possible to capture a signal smaller than the size of the quantization step—ironically known as the least significant bit. Small signal changes have to jump up to the nearest quantization level. Larger bit depths have smaller quantization steps and thus smaller levels of noise amplification.
Most importantly though, note that the amplitude of quantization noise remains consistent, regardless of the amplitude of the input signals. This demonstrates that noise happens at all the different quantization levels, so there’s a consistent level of noise for any given bit-depth. Larger bit depths produce less noise. We should, therefore, think of the differences between 16 and 24 bit depths not as the accuracy in the shape of a waveform, but as the available limit before digital noise interferes with our signal.
Bit depth is all about noise

Kelly Sikkema We require a bit-depth with enough SNR to accommodate for our background noise to capture our audio as perfectly as it sounds in the real world.
Now that we are talking about bit depth in terms of noise, let’s go back to our above graphics one last time. Note how the 8-bit example looks like an almost perfect match for our noisy input signal. This is because its 8-bit resolution is actually sufficient to capture the level of the background noise. In other words: the quantization step size is smaller than the amplitude of the noise, or the signal-to-noise ratio (SNR) is better than the background noise level.
The equation
20log(2n), where n is the bit-depth, gives us the SNR. An 8-bit signal has an SNR of 48dB, 12 bits is 72dB, while 16-bit hits 96dB, and 24 bits a whopping 144dB. This is important because we now know that we only need a bit depth with enough SNR to accommodate the dynamic range between our background noise and the loudest signal we want to capture to reproduce audio as perfectly as it appears in the real world. It gets a little tricky moving from the relative scales of the digital realm to the sound pressure-based scales of the physical world, so we’ll try to keep it simple.
CD-quality may be “only” 16 bit, but it’s overkill for quality.
Your ear has a sensitivity ranging from 0dB (silence) to about 120dB (painfully loud sound), and the theoretical ability (depending on a few factors) to discern volumes is just 1dB apart. So the dynamic range of your ear is about 120dB, or close to 20 bits.
However, you can’t hear all this at once, as the
tympanic membrane, or eardrum, tightens to reduce the amount of volume actually reaching the inner ear in loud environments. You’re also not going to be listening to music anywhere near this loud,
because you’ll go deaf. Furthermore, the environments you and I listen to music in are not as silent as healthy ears can hear. A
well-treated recording studio may take us down to below 20dB for background noise, but listening in a bustling living room or on the bus will obviously worsen the conditions and
reduce the usefulness of a high dynamic range.
The human ear has a huge dynamic range, but just not all at one time. Masking and our ear's own hearing protection reduces its effectiveness.
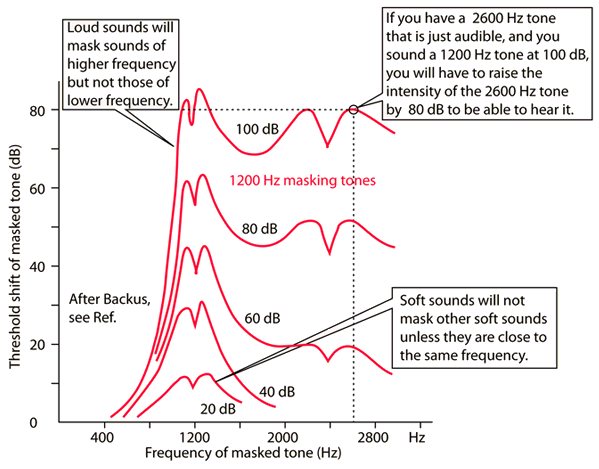
On top of all that: as loudness increases, higher frequency masking takes effect in your ear. At low volumes of 20 to 40dB, masking doesn’t occur except for sounds close in pitch. However, at 80dB sounds below 40dB will be masked, while at 100dB sound below 70dB are impossible to hear. The dynamic nature of the ear and listening material makes it hard to give a precise number, but the real dynamic range of your hearing is likely in the region of 70dB in an average environment, down to just 40dB in very loud environments. A bit depth of just 12 bits would probably have most people covered, so 16-bit CDs give us plenty of headroom.
hyperphysics High-frequency masking occurs at loud listening volumes, limiting our perception of quieter sounds.
Instruments and recording equipment introduce noise too (especially guitar amps), even in very quiet recording studios. There have also been a few studies into the dynamic range of different genres, including
this one which shows a typical 60dB dynamic range. Unsurprisingly, genres with a greater affinity for quiet parts, such as choir, opera, and piano, showed maximum dynamic ranges around 70dB, while “louder” rock, pop, and rap genres tended towards 60dB and below. Ultimately,
music is only produced and recorded with so much fidelity.
You might be familiar with the music industry “
loudness wars“, which certainly defeats the purpose of today’s Hi-Res audio formats. Heavy use of compression (which boosts noise and attenuates peaks) reduces dynamic range. Modern music has considerably less dynamic range than albums from 30 years ago. Theoretically, modern music could be distributed at lower bit rates than old music. You can check out the
dynamic range of many albums here.
16 bits is all you need
This has been quite a journey, but hopefully, you’ve come away with a much more nuanced picture of bit depth, noise, and dynamic range, than those misleading stair-case examples you so often see.
Bit depth is all about noise, and the more bits of data you have to store audio, the less quantization noise will be introduced into your recording. By the same token, you’ll also be able to capture smaller signals more accurately, helping to drive the digital noise floor below the recording or listening environment. That’s all we need bit depth for. There’s no benefit in using huge bit depths for audio masters.

Alexey Ruban Due to the way noise gets summed during the mixing process, recording audio at 24 bits makes sense. It’s not necessary for the final stereo master.
Surprisingly, 12 bits is probably enough for a decent sounding music master and to cater to the dynamic range of most listening environments. However, digital audio transports more than just music, and examples like speech or environmental recordings for TV can make use of a wider dynamic range than most music does. Plus a little headroom for separation between loud and quiet never hurt anyone.
On balance, 16 bits (96dB of dynamic range or 120dB with dithering applied) accommodates a wide range of audio types, as well as the limits of human hearing and typical listening environments. The perceptual increases in 24-bit quality
are highly debatable if not simply a placebo, as I hope I’ve demonstrated. Plus, the
increase in file sizes and bandwidth makes them unnecessary. The type of compression used to shrink down the file size of your music library or stream has a much more noticeable impact on sound quality than whether it’s a 16 or 24-bit file.